探偵ホームズと刑事コロンボの推論方法

活動日誌について

今話題の科学情報やイベント、技術などについての話し合いや考察を、レポート形式でまとめて配信しています！学生ならではの視点でまとめているので、理系の知識が少ない人にも、解りやすく解説出来るように日々つとめておりますので、お気軽にご意見・ご感想を頂けますと幸いです！

セラミックスフィーバーケミカルアタックブリードアウトムーンライト計画

2014 03/12

科学と技術

「問題解決」は科学と技術にとって大切です。「問題解決」の方法を理解すれば「考え方」の使い分けができ、よりスムーズに、視野を広げて、様々な問題を解決出来ます。探偵物を例に「問題解決」の方法を探ってみましょう。（有栖木智恵）

問題解決技術科学

report of

対話

ふっふっふっふっふっ！

「真実はいつも１つ！」

なんですか？あれ。
いつもに増して
妙にテンション高い人が
いるんですけど。

しらん。

ふふふ、

ふっふっふっ！

溜まってた課題が全部終わって
今週は、買いだめ撮りだめしてた
漫画とアニメ解禁週間中！
なんですよー！
ヲタ充ー！

あー。すぐこれだ。
部活はどうすんだよ。

理佳先輩、手伝わない方が
良かったんじゃないですか？

そんなー！

みんなもこれ
貸してあげるから！
一緒に読もうよ！

ふふふ、すごい
たくさんの漫画。

何の漫画だ？

「名探偵コナン」ですよ！
ゴールデンウィーク前あたりに
新作の映画も公開されるんですよー！
みんなで見に行きましょうよ！

お！いいな！

理佳先輩まで乗り気になって
どうするんですか・・・
ミイラ取りがミイラ・・・

でも、なんでまた？

先週、理佳先輩が
「真実はいつも一つ！」
って言ってたじゃないですか！
それ聞いたら、無性ーに
読みたくなっちゃって！

文子先輩って
影響されやすいタイプですよね。

騙されないように注意しろよ

ふふふ、高い壷とか
買わされないようにね。

それどういう意味ですかね・・・
まぁ良いですけど・・・

それより
探偵物って面白いですよね！
推理するのが楽しいっていうか
謎が解けたときの爽快感！

文子先輩に
推理や謎解きが
できるんですか？

推理、謎解きが得意だったら
あんなに課題の問題解決に
時間使わないだろ。

なんか最近
私に対する
みんなの風当たり
強くない・・・？

ふふふ、

でも、そうね、問題解決について
「探偵小説」で説明すると
少し、分かりやすいかもしれない。

問題解決って
先週の話の続きですか？

そうね。

さすが私！そのつもりで
この漫画を持ってきたんですよ！

いや、嘘だろ。

さっき思いっきり
ヲタ充ー！とか
叫んでたじゃないですか。

真実は、たまに２つ！

いや、ごまかしてもだめだから。

みんなひどいよー・・・・

でもなんで問題解決の説明が
探偵小説なんだ？

科学で重要な
「論理学」について
哲学者による議論が
活発に行われていた時代に
探偵小説が生まれているの。

ほぇー！それって
いつ頃なんですか？

現在の、論理学の体系が
ほぼできあがった頃ぐらいかしらね。
1841年に、探偵小説の元祖
エドガー・アラン・ポーの
「モルグ街の殺人」が、発表されているの。

探偵小説の元祖！
エドガー・アラン・ポー！

って、だれですか？

おいおい
冗談だろ？！

コナンでもおなじみの
江戸川乱歩先生の筆名の元となった
とも言われる、アメリカの文豪
エドガー・アラン・ポーだろ！

えぇ？！
江戸川コナンの名前の元の
江戸川乱歩さんの名前のさらに元に
モデルがいらっしゃったなんて！

文子先輩、本当に「名探偵コナン」
ちゃんと読んでるんですか？

あ！ちょっと待って下さい！
1840年ごろのアメリカですか？？

それなら、先週私が課題で悩まされた
「マッハ力学史」の著者で
物理学者のエルンスト・マッハさんが
活躍した頃ですね！！

・・・・
エルンスト・マッハさんは
オーストリアじゃ無かったかしら？
それに、生まれたのって
ちょうど1840年頃
だったんじゃないかしら？

ふふふ
エルンストさん
まだ、赤ちゃん。

あれ・・・？

文子、今、ドヤ顔してたよな。

文子先輩恥ずかしー。

えー・・・・っと・・・・
ぁぅ・・・・・
きっとマッハさんなら
赤ちゃんのころから
頭よくて活躍出来たはずです・・・

そんなことがあるわけないじゃないですか。

話は戻るけど
エドガー・アラン・ポーなら
「黄金虫」とかが有名だな。

謎解き物語として
有名な作品ね。

有名どころで言えば、私は
「シャーロックホームズシリーズ」
が好きです！
コナンの名前の元の
アーサー・コナン・ドイルの！

そう、ね。
エドガー・アラン・ポーの
「モルグ街の殺人」に出てくる
探偵デュパンよりも
探偵ホームズのほうが
洗練された分析的思考で
事件の推理を行っていると
言われているの。

そうなんですか！
ちなみに、智恵先輩は
どのシリーズが好きですか？

そうね・・・

私は、おじ様の探偵の
刑事コロンボさんが
好き、かしら。

渋いな！
あのちょっと
何考えてるか分かんない感じの
オヤジ探偵か？
某番組でよく再放送してたな。

名前だけは聞いたことあります！

そうね。
ロサンゼルス市警察、殺人課の
警察官コロンボを主人公とした
サスペンスドラマなの。

「ウチのかみさんがね」っていう
台詞が有名なんだよな！

ここは探偵物オタクの
集まりですか？
なんか趣旨が
どんどんかけ離れて
いってますよ。

ふふふ、

じゃあ、せっかくだから
探偵ホームズと
刑事コロンボを
例に、問題の解き方を
比較してみましょうか？

私、あんまり探偵物
読まないんですけど
私でも分かりますか？

私もあんまり探偵物
分かんないです！

文子先輩の場合
分かる話題って
あるんですか？

あ、あるってば！

じゃあ、なるべく
分かりやすく
説明出来るように
がんばりましょう。

あたしは割と分かるぞ！

探偵ホームズシリーズの特徴としては
読者と同レベルの観点の語り手
である、ワトソン医師がいて
物語展開は、見事なぐらい
ワンパターンだよな。

ふふふ、
そうね。

ストーリー展開としては
ベーカー街で物語は始まって
そこへ依頼人が登場して
謎が提起される。

それを受けて、仮説をたてた
探偵ホームズとワトソンは
分析と調査に乗り出し
証拠を通して
事件を順々に解明して行き
謎を解決する
っていうパターン。
ってところか？

もし、最初の仮説で
うまくゆかない時には
ベーカー街の事務所に戻り
依頼人から、再度話を聞くか
推理をやり直すのね。

それって結局
どういうことですか？

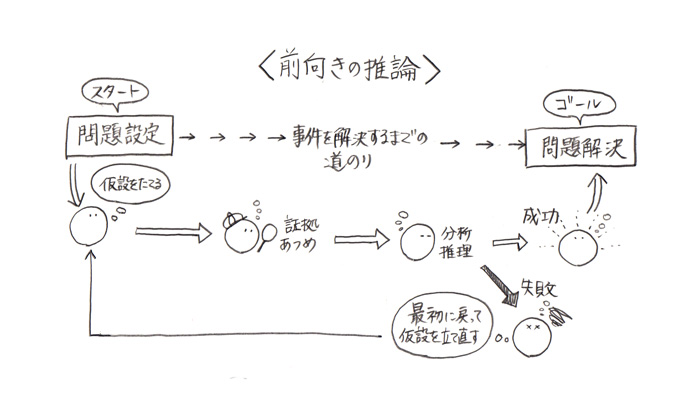
まず始めに
ベーカー街で「問題設定」し
仮説をたてて、

次に、その問題を
論理的に、前向きに
「分析的思考」で推理して
仮説に準ずる証拠あつめを
していくの。

最後に、見つけた証拠をつないでゆき
犯人にたどりつく
つまり「問題解決する」
と、なるんじゃないかしら。
もし結論にたどり着かない場合は
最初に戻って仮説を立て直すのね。

図で書くとこんな感じか？

まず始めに
問題を定義し仮説をたてるだろ？
その次に論理的に分析して推論し
問題を解決する。

「前向き」に進んでいってるな。

なるほど。。。
なんとなく
分かった気がします。。。

これが、現在普及している
科学的問題解決法の
典型的なプロセスってことを
言いたいんですか？

ふふふ、
そうね。
それに、

「ただ一滴の水から、論理家は、大西洋やナイアガラ瀑布など見たり聞いたりしたことがなくても、存在の可能なことを推定しうるであろう」

って言う、ホームズ探偵の
壮大なセリフがあるのだけれど
それは、研究分野でよく使われている
「一般的原理から個々の事柄の正しさを推論する」
演繹的推論と呼ばれる
科学的な「考える技術」と同じなの。

へぇー
そういう観点でみるのも
おもしろいな

ぅーん？

「一滴の水」が
目の前に存在しているという事実を
確認出来れば
それの集合体である
大西洋やナイアガラも
存在可能ってことが解る
ってことですよね。

おお、なるほど。

探偵ホームズは
科学的論理学が成立した
１９世紀に書かれた小説だから
その成果が、小説にたくさん
盛り込まれているわ。

ホームズは名言いっぱいあるよな！

そうね、

「だいたい犯罪にはきわめて強い類似性があるから、千の犯罪を詳しく知っていれば、千一番目のものが解決できなかったら不思議なくらいなものだ。」

というセリフもあるの。

それはさっきの、演繹的推論とは異なる
「個々の事実から一般的原理（法則）を導く推論」で
多くの個々の情報から、１つの結論を「推測」する
帰納的推論と呼ばれているの。

むむむ？？

ふふふ、
ちょっと、難しかったかしら。
ごめんなさいね。

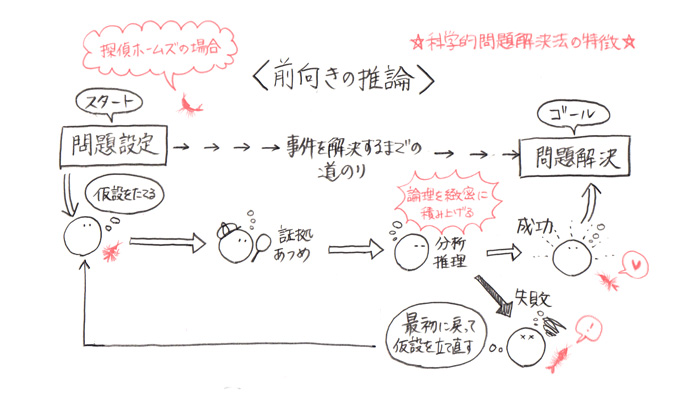
探偵ホームズは
科学的問題解決法を駆使して
事件を解決していたってことだ。

うーん。。。

要するにまとめると
探偵ホームズの場合
科学的問題解決法の特徴である
前向きの推論で
ストーリーが展開されていて
その推理の過程で
科学的問題解決法で重要な
帰納的推論や演繹的推論
が駆使されている
ってことですね。

そうね、さすが
めかちゃん。

べつにこれぐらいふつうです。

なるほど。。。
何となく分かった気がします！

じゃあ、コロンボはどうなんですか？

刑事コロンボは
倒叙探偵小説という
ジャンルの物語なの。

倒叙？？

倒叙探偵小説は
物語の展開が
探偵ホームズと全く逆で
事件から物語が始まっている
お話のことなの。

そういえば刑事コロンボの場合
視聴者にあらかじめ犯人が分かっちゃうよな。

そう、ね。
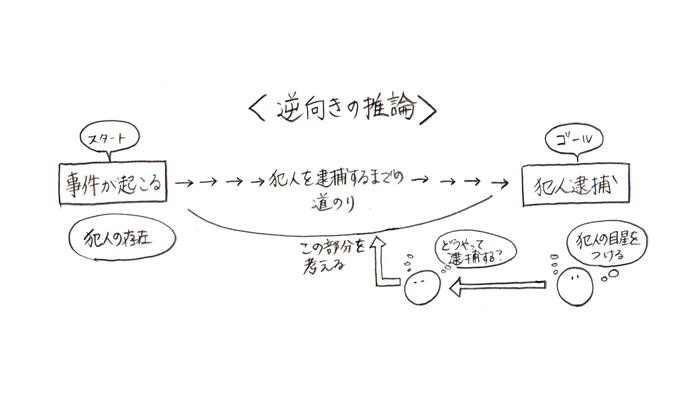
だから 一般的な探偵小説のように
探偵が分析した結果から
前向きに推論を展開して
犯人に関する事件の情報を
探す形式を、とることができないの。
物語は、最初に提示された
犯人の情報から、どのような
犯人逮捕のシナリオとなるのか
考える形式になるの。

これは 一般の探偵小説を
逆向きに推理を展開するようなもの
と、言えるんじゃないかしら。

まず事件が起こり、視聴者に
事件の一部始終が公開されてしまうので
どのように犯行が行われていったかを
推理して犯人を突き止めるのではなく
犯行を行った犯人をどのようにして
追い込んでいくのかを推理する
ということになるんですね。

図で書くとこんな感じか？

事件がおこって
犯人の目星がついてて
犯人逮捕という「問題解決」のゴール
がここにあって
それを捕まえるにはどうしたら良いか
って考えるってことだろ？

なるほど・・・
逆から見てますね。

さっきから、言おうか
迷ってたんですけど
それ、なんですか？
図の中にいる、わけの解らない
まるい変なの・・・

変とは失礼な！

どっからどう見ても
まりもだろ。
かわいいだろ！

まりも・・・？
いや、ますます
意味解んないですから

話は戻りますけど
さっきの前向きの推論が
科学的問題解決方法
っていうことは
その逆向きの推論が
技術的問題解決方法
っていうことですか？

ふふふ、そうね。
でも、それだけじゃないのよ。

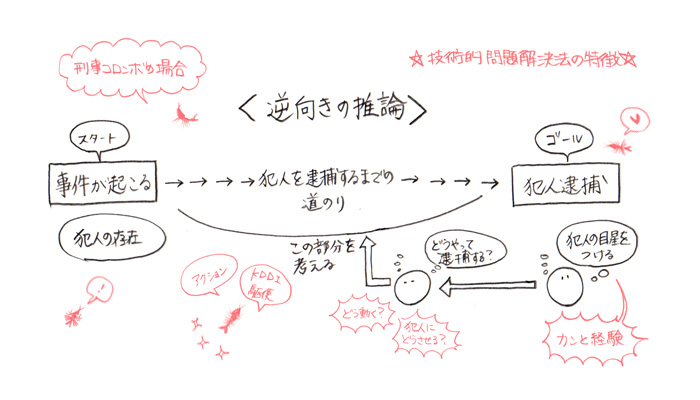
コロンボは刑事は、「カン」を
たよりに探っていくことが
多々あるの。このあたりは
論理を緻密に積み上げて
犯人を追い詰めてゆく
ホームズと、大きく異なる
点じゃないかしら。
それに、コロンボはいつも
犯人に直接関係する「アクション」を
重視しているの。

犯人に直接関係する「アクション」？

例えば、証拠が何も無いときに
犯人かもしれない、確証のない人を
逮捕するのは難しいでしょ？

そうですね！
証拠品は推理ものの
必需品ですよね！

でも、それが無い場合
どうしましょうか？

そうだなー。
あとは怪しい行動とかか？

ふふふ、そうね。
犯人しか知らない行動をとったら
その人を犯人と決めることが
出来るかもしれないわね。

確かにそうですね。

そこでコロンボは、実験するの。
証拠は無いけど、「犯人」と
目星を付けた人に
犯人しか知らない
アクションを起こさせるための情報を
教えるの。

なるほど！そうすれば
もしその人が犯人なら
その情報によって、何かしらの
アクションを起こして
犯人を確保することが出来ると！

そういうことね。

具体的にどういう事件なんですか？

ふふふ。
それは、実際に
見てのお楽しみ、ね。

うちの大学の図書館にも置いてあったよ。
後で借りてくれば良いんじゃないか？

私はここの学生じゃないんで
借りれないんですけど。

でも、話はもどりますけど
刑事の「カン」ってことは
先日の話でもでた
KKDってことですよね！
そこも技術的な問題解決法の特徴
ってことですか！

ふふふ、そうね。
それだけじゃなく
刑事のカンから推定されたことから
犯人につながるアクションを起こさせる
と、いうことも
技術的な問題解決法に
通じるんじゃないかしら。

それってどういうことだ？

「技術」において
機能実現を確認する実験が
不可欠なの。
だから、コロンボのように
「犯人確保」である結論から
逆向きに、その結論に至るアクションを
考えるような問題解決の方法が
「技術」では重要なの。

科学では、仮説を設定して
その仮説の正しさを確認するために
やはり実験を行うけど
技術では、アイデアが
正しく機能するかどうかを
確認するために実験をするってことか。

そう、ね。

だから科学では
前向きに推論を進めることが多いけど
技術では必要な機能から逆向きに
それを実現するために
取るべきアクションを考えるスタイル
になるってことですか。

そうね。
めかちゃんの言う通り
技術ではいつも
機能から逆向きに考えるスタイルが
問題解決法の特徴になっているの。

なるほど。

でも科学でも
結論から逆向きに考えると
問題の見通しがよくなる
と、言われているのよ。

臨機応変に思考を使い分けろってことだな。

柔軟性って大事ですね。

そうだぞめか。
もっと柔軟になった方が
良いんじゃないか？

どういうことですか？
余計なお世話です！

ふふふ、

こんな感じで
解ったかしら？

そうですね！一口に探偵物、推理物
って言っても、作品によっては
色々な技法が使われていて
面白いなって思いました！
あと、作品の時代背景とかも感じられて
とても勉強になりました！

今日の論点はそこじゃないだろ。

ふふふ、
でも、文子ちゃんの
言ったところも
大切なところね。

せっかくだから、文子先輩
今日の話、まとめて下さいよ。

ええ？！

そうだなあ
ええっと・・・・

科学的問題解決法の特徴は
探偵物に例えると
「シャーロックホームズ」の様に
事件という「問題」から
論理を緻密に積み上げて
犯人を追い詰め「解決」までたどり着く
前向きの推論で行わることが多くて、

技術的問題解決法の特徴は
探偵物に例えると、「刑事コロンボ」の様に
勘と経験で目星をつけた犯人を
逮捕するという「問題解決」のために
どう動くか、どうさせるか
というアクションを、KDDを駆使して考える
いわば、結論から逆向きに推論する方法をとる。

でも、臨機応変に
「考え方」の使い分けをすれば
よりスムーズに、視野を広げて
問題を解くことが出来る！

ってなまとめでどうでしょうか。

ちなみに図はこんな感じで！

ふふふ、そうね。
伝わって、良かったわ。

まぁ、だいたいそんなとこだろうな。
文子にしては上出来じゃん。

確かにそうですけど・・・・
文子先輩、何ですか？
その図の端の
ゴ●ブリみたいなの・・・

かわいいまりもの横に
そんな不気味な物書くなよ。

ふふふ、
げじげじ？

え！どっからどう見ても
マリモと戯れる
小エビちゃんですよ！
最近よく売ってるじゃないですか！
観賞用の可愛い小エビ！！！

え。

え？

ふふ、

みんな・・・ひどい・・・

2014年3月12日：関連ページ

【関連対話】
科学と技術 001：これからの「科学」と「技術」に向き合う姿勢
– – – – – – – – – –
科学と技術 002：「未来技術に必要なこと」は何なのか
科学と技術 003：探偵ホームズと刑事コロンボの推論方法（現在の記事です）
科学と技術 004：コロンボとホームズの推理対決!

コチラの記事もどうぞ

コロンボとホームズの推理対決! もし推論方法の違う有能な探偵二人が推理対決をしたらどちらが勝つのでしょうか！！問題解決方法の観点からみんなで勝敗の行方を想像してみました！ […]
「未来技術に必要なこと」は何なのか発明や発見が、世の中に認められるには「科学的証明」が必要不可欠です。では、「未来技術」を発展させるには、何が必要なのでしょうか？部員のみん […]
これからの「科学」と「技術」に向き合う姿勢「STAP細胞」で話題になったリケジョの「小保方さん」。彼女の素晴らしい発見について部内でも話題になりました。彼女のケースと、同じ万能細胞 […]
未来を変える万能生物？ミドリムシ？今何かと注目されているミドリムシ。健康に良いとされ、様々な健康食品に使用されているだけでなく、最近発表された、「燃料」としての使用法も期待 […]